
幂法用于求解矩阵的按模最大特征值,当矩阵$\textrm{A}$的$\textrm{n}$个特征值线性无关时,任取一组初始向量$u_0$,对其不断做运算$u_{k+1}= A*u_k$,最终就会有$u_{k+1}/u_k = λ_{|max|}$,其原理是一种极限的思想,当迭代次数足够多时,其他特征值相对比$λ_{|max|}$几乎为0。而反幂法则是将所有特征值取倒数,通过求解此时的最大按模特征值,再取倒数回来,从而得到按模最小特征值。两种方法在大量的博客或文库中有详细的说明,不熟悉可以点击这里进行阅读。幂法和反幂法本身只能求解矩阵按模的最大与最小特征值,但这两个方法的应用远不止此。通过与原点平移法相结合,反幂法可以求解矩阵的任何特征值。首先大致阐述一下原点平移法的原理。
首先考虑这样一个问题,如果有一组数组$A$满足$A_0 < A_1 < A_2 < …… < A_n$,将该数组以绝对值排序,那么谁有可能成为按模最大的值?显然只有$A_0$与$A_n$有可能。那么再考虑新的问题,如果是先将这$n$个数同时加上一个实数$k$,得到$A_0+k,A_1+k,A_2+k,……,A_n+k$,再以绝对值排序,那么哪些数有可能成为按模最大值?答案仍然是$A_0$与$A_n$。
我们任取一个数$A_k$,其中$0< k< n$,于是相当于$a < b < c$,不妨讨论他们的正负性。$k > 0$时,若$c > 0$ and $b > 0$,则一定有$|c+k| > |b+k|$,否则一定有$|a+k| > |b+k|$。如果$k < 0$则是完全对称的情况,若$a < 0$ and $b < 0$,则一定有$|a+k| > |b+k|$,否则$|c+k| > |b+k|$一定成立。综上所述,一组数列同时加上任意实数$k$然后再按绝对值排序,能够得到的按模最大值只会是$A_0或A_n$。
然后再考虑新的问题,若将数组$A$以绝对值排序,谁有可能成为按模最小值?我们无从得知,因为可能是每一个数。
而如果,将这$n$个数同时加上一个实数$k$,得到$A_0+k,A_1+k,A_2+k,A_3+k,……,A_n+k$,再以绝对值排序,同样地,每一个数都有可能成为按模最小值。更具体的,如果$k = -A_i$,那么$A_i$将成为新数组的最小按模值,因为$|A_i+k| == 0$,而其他数均为非零数,故得证。于是我们可以得出结论:对于数列$A$,若其满足$A_0 < A_1 < A_2 < …… < A_n$,那么将其每个项加上$k$再按绝对值排序之后
- 只有$A_0与A_n$能成为按模最大值
- 每一个项都有可能成为按模最小值,特别地,当$ A_i-(A_i-A_{i-1})/2< k < A_i+(A_{i+1}-A_i)/2$时,$A_i$为最小按模值。
原点平移法的原理便是,将矩阵的主对角线全部加上一个数$k$,然后求该新的矩阵的特征值。由公式$|A-λE| = 0$可知,新矩阵$A+kE$的特征值方程即为$|A-λE+kE| = 0$,于是新矩阵的特征值就是原矩阵的全部特征值分别加上$k$得到的数列。综合上述的结论可知,对于幂法,原点平移法可以改变其迭代的最终结果,但值域仅限于最小与最大按模特征值。而对于反幂法,如果能够枚举出合适的$k$,是可以计算出每一个特征值的。在确保该思想能够正确进行之前,我们首先回到幂法,保证幂法能够正确进行。
考虑一下幂法什么时候无法计算出答案?一般情况有两种:第一种是存在两个互为相反数的最大特征值,该情况的解决方法是用$X_{k+2}:X_k$来判定,但我们也可以通过平移法使得这两个最大特征值不再互为相反数,例如某矩阵的按模最大特征值为$\textrm{5}$和$\textrm{-5}$,那么我们平移任意一个足以区分两数的距离,例如$\textrm{1}$,那么 变为$\textrm{6}$和$\textrm{-4}$,此时便转换成了一般情况;第二种是迭代次数过大,针对这种情况,我们就需要用到上述的原点平移法。决定幂法迭代次数的因素是最大按模特征值与次大按模特征值的比值,这个比值会随着迭代不断增大,但是增大的幅度是不确定的,我们可以通过平移的方法增大这个比值的初始值来加速迭代。
我们已经得出了结论,按模最大值只可能是$A_0与A_n$中的一个,所以按模次大值可以看做原数列去掉按模最大值后新的按模最大值,显然按模最大值是$A_0$时,按模次大值可能是$A_1或A_n$;而$A_n$是按模最大值时,$A_0与A_{n-1}$可能是按模次大值,于是我们的关注点在四个数上,即$A_0,A_1,A_{n-1},A_n$,按模最大与次大值一定在这四个数中产生。此外,随着原点平移值的变换,按模最大值与次大按模值是可能发生改变的,变幻的趋势取决于这四个数的正负性。所以我们需要讨论他们的正负性和各种绝对值排序情况。
考虑$0$在$A_0,A_1,A_{n-1},A_n$可以插入的位置,四个数有五个空位,因此$0$的分布有五种情况,即
- $0,A_0,A_1,A_{n-1},A_n$
- $A_0,0,A_1,A_{n-1},A_n$
- $A_0,A_1,0,A_{n-1},A_n$
- $A_0,A_1,A_{n-1},0,A_n$
- $A_0,A_1,A_{n-1},A_n,0$
而对于每种情况,谁为按模最大值和按模次大值又可以继续进行分类,对于上述$5$种$0$的分布情况,我们其命名为$Group_1$至$Group_5$,那么一共有如下$\textrm{12}$种情况:
| Number | Group | 按模最大值 | 按模次大值 |
|---|
| $1$ | $1$ | $A_n$ | $A_{n-1}$ |
| $2$ | $2$ | $A_n$ | $A_{n-1}$ |
| $3$ | $2$ | $A_n$ | $A_0$ |
| $4$ | $2$ | $A_0$ | $A_n$ |
| $5$ | $3$ | $A_n$ | $A_{n-1}$ |
| $6$ | $3$ | $A_n$ | $A_0$ |
| $7$ | $3$ | $A_0$ | $A_n$ |
| $8$ | $3$ | $A_0$ | $A_1$ |
| $9$ | $4$ | $A_n$ | $A_0$ |
| $10$ | $4$ | $A_0$ | $A_n$ |
| $11$ | $4$ | $A_0$ | $A_1$ |
| $12$ | $5$ | $A_0$ | $A_1$ |
尽管有$\textrm{12}$种分布情况,但其实他们的图像分布是有对称性的,例如$Num_1$与$Num_{12}$是对称的,我们针对每种情况,列举一种特殊值,以平移距离$\textrm{k}$为横坐标,以平移之后的按模最大值与按模次大值的比的绝对值为纵坐标,通过$\textrm{Python}$绘制可视化图像
import numpy as np
import matplotlib.pyplot as plt
#v is A[0],A[1],A[n-1] and A[n]
#s is the title of graph
def graph(v:list, s:str):
x = [] #record the value of translation
y = [] #record the value of abs(max/second-max)
for i in range(-20,20):
a = [abs(e+i) for e in v]
a.sort() #sort with the key that using abs value
x.append(i)
y.append(a[-1]/a[-2])
plt.plot(x,y)
plt.title(s)
plt.xlabel("k")
plt.ylabel("value")
plt.show()
观察这$\textrm{12}$个图像可以发现他们都有一个共同点,即先单调递增,然后单调递减,然后再单调递增,最后再单调递减。并且当$\textrm{k}$趋近于两端无穷时,比值无限接近于$\textrm{1}$。再注意到图像有两个峰值,上述提到过,随着平移距离的变换,矩阵的按模最大特征值是可能易主的,但也只会在$A_0$与$A_n$之间变换。而两个峰值对应的就是$A_0$与$A_n$的最大加速点,至于对应关系要视情况而定。至于为何有多段单调递增与递减区间,是因为按模最大值与按模次大值都在变换的缘故,举个例子,若有$A_0,A_1,A_{n-1},A_n=\{-8,-6,12,15\}$,这是$Num_5$的情况,从$\textrm{0}$开始,$\frac{15+k}{12+k}$的比值不断减小,最终极限值为$\textrm{1}$;而当$k < 0$时,一开始比值得到了增大,但$k = -2$时,此时$abs(-8-2) = 10,abs(12-2) = 10$,$A_0与A_{n-1}$具有相同的绝对值了,此时$\textrm{k}$再减小,次模最大值便要换成$A_0$了,那么函数变为单调递减;而$\textrm{k = -3.5}$时,此时按模最大值也换人了,变成了$A_0$,按模次大值变成了$A_n$,函数又迎来了单增,最后$\textrm{k = -4.5}$时,按模次大值变成$A_1$,从此之后,函数边一直单减,并在极限处趋近于$\textrm{1}$。
$\textrm{12}$种情况讨论显然过于复杂,我们可以以图像在$x = 0$的导数$f'(0)$与$0$的大小关系进行区分,并将结果与之前的表格结合,得到如下结果:
| Number | Group | 按模最大值 | 按模次大值 | $f'(0)$ |
|---|
| $1$ | $1$ | $A_n$ | $A_{n-1}$ | - |
| $2$ | $2$ | $A_n$ | $A_{n-1}$ | - |
| $3$ | $2$ | $A_n$ | $A_0$ | + |
| $4$ | $2$ | $A_0$ | $A_n$ | - |
| $5$ | $3$ | $A_n$ | $A_{n-1}$ | - |
| $6$ | $3$ | $A_n$ | $A_0$ | + |
| $7$ | $3$ | $A_0$ | $A_n$ | - |
| $8$ | $3$ | $A_0$ | $A_1$ | + |
| $9$ | $4$ | $A_n$ | $A_0$ | + |
| $10$ | $4$ | $A_0$ | $A_n$ | - |
| $11$ | $4$ | $A_0$ | $A_1$ | + |
| $12$ | $5$ | $A_0$ | $A_1$ | + |
简要分析便可以看出,结果具有高度的对称性,每一个结果为+的图像均可以找到一个结果为-的图像使得两个图像的单调性关于$y$轴对称。因此我们仅讨论$f'(0) > 0$的图像,剩余的$\textrm{6}$个完全可以参照他们对应的对称图像。这样我们通过$f'(0)$这个参数便把图像规模减少了一半,继续考虑剩下的$\textrm{6}$个图像。
| Number | Group | 按模最大值 | 按模次大值 | $f'(0)$ |
|---|
| $3$ | $2$ | $A_n$ | $A_0$ | + |
| $6$ | $3$ | $A_n$ | $A_0$ | + |
| $9$ | $4$ | $A_n$ | $A_0$ | + |
| $8$ | $3$ | $A_0$ | $A_1$ | + |
| $11$ | $4$ | $A_0$ | $A_1$ | + |
| $12$ | $5$ | $A_0$ | $A_1$ | + |
可以发现,$Num_3,Num_6,Num_9$的按模最大值均是$A_n$,按模次大值$A_0$,而剩余的三个图像按模最大值是$A_0$,按模次大值均是$A_1$。并且注意到前三者的$Group$分别为2,3,4,这就意味着$A_n > 0,A_0 < 0$,同样后三者也有$A_0 < 0,A_1 < 0$。结合图像,我们发现这些函数的初始按模最大值均是$\textrm{0}$的右侧第一个峰值;更具体的,前三者的函数在$x=0$的右侧只有一个峰值,而后三者有两个,我们希望能找到一种通用算法,来求出这两种图像的右侧第一个峰值。
模拟退火的算法应用于此有些复杂冗长,因此这里采用第二种算法$\textrm{:}$快慢双指针,我们令$\textrm{Fast = 0.1,Slow = P}$,在$\textrm{Fast < Slow}$时,不断迭代$\textrm{Fast *= 1.1,Slow *= 0.9}$。那么无论沟壑的分布位置如何,基于该算法几乎可以完成所有类似分布的探测。尽管仍然存在极少数极端数据可能使得该算法失效,但该算法已经占比降低到了比较理想的状况。。
最后还有一个问题,我们上述图像使用的$\textrm{Y}$值是最大按模值与次大按模值的比值,但是在实际迭代的时候,我们并不知道该比值的大小,因此我们采用另一个变量来取代之$\textrm{:}$在检测最佳平移距离的时候,我们修改最大迭代距离至一个比较小的值,例如$\textrm{100}$,然后在迭代$\textrm{100}$次之后,构造这样一个数组$\{A_0^{100}/A_0^{99},A_1^{100}/A_1^{99},……,A_n^{100}/A_n^{99}\}$,然后计算这个数组的方差,对于已经快完成迭代的数组,这个方差应该越接近于$\textrm{0}$,因此我们用迭代完成的最后两个向量的比值构造的数列的方差来替代上述图像的$\textrm{Y}$坐标值。
至此,我们已经尽可能的对幂法进行加速优化,假定通过上述理论能够求解任意一般矩阵的按模最大特征值,那么基于这个前提,我们开始讨论如何使用反幂法求解一个矩阵的全部特征值。同样地,我们首先考虑反幂法什么时候会无法得到解,因为反幂法的算法设计三角分解,因此$\textrm{LU}$矩阵若不能正确分解,那么反幂法是不能进行的,查询得知一个矩阵存在$\textrm{LU}$分解的充要条件是其各阶顺序主子式均不为零。实际计算的时候,如果对每个矩阵都进行各阶顺序主子式的行列式计算需要过高的复杂度,因此采用了另一种方案,计算过程中不存在$\textrm{LU}$分解的表现为$\textrm{LU}$矩阵中存在$\textrm{inf}$与$\textrm{nan}$元素,那么在$\textrm{c++}$中可以通过$\textrm{isnan()}$与$\textrm{isinf()}$函数来检测一个$\textrm{double}$是否是$\textrm{nan}$和$\textrm{inf}$, 所以我们直接进行分解,再分解的过程中对每个元素调用$\textrm{isnan()}$与$\textrm{isinf()}$,如果有一个元素的检测结果为$\textrm{true}$,那么我们认为这个矩阵不能进行三角分解。此外,反幂法同样可能存在迭代次数过大的情况,但反幂法的最佳平移距离的 讨论过于复杂。我们先假定一个比较理想的情况,就是反幂法都可以在设定的最大迭代次数内求解,并且任意设置的平移距离都存在$\textrm{LU}$分解。
我们在上述提到过当平移距离$k$满足$ A_i-(A_i-A_{i-1})/2< k < A_i+(A_{i+1}-A_i)/2$时,$A_i$为最小按模值,也就是说在$A_i$的左右区间内都存在一段距离,在该距离的取值都将使按模最小值指向$A_i$,所以做法很明显了:分治。通过对幂法的加速讨论,我们假定可以求出矩阵的最大按模特征值为$\textrm{maxv,}$那么设定$\textrm{left = -|maxv|,right = |maxv|}$,通过一段伪代码来说明其原理$\textrm{:}$
double getMinEigenValue(double translationDistance)
{
/*procssing*/
return 按模最小特征值 based on translationDistance;
}
void solve(double left,double right)
{
if(getMinEigenValue(left) == getMinEigenValue(right))
{
result.insert(thisEigenValue);
}
double mid = (left+right)/2;
solve(left,mid);
solve(mid,right);
}
$\textrm{getMinEigenValue}$是在平移了指定距离之后得到的按模最小特征值,当得到一段区间的时候,我们检测其两端的最小按模特 征值是否一致,若是,那么这个特征值已经被确定,将其加入到结果中;否则以中点为划分,继续递归两个子区间。
算法的思想很简单,但是实际操作的时候还是有一些细节问题要处理,最主要的还是精度问题,假定有一个特征值$\textrm{20.5}$,我 们在平移距离为$\textrm{20}$的时候,计算出来的结果可能是$\textrm{20.4475634,}$在平移距离为$\textrm{21}$时候计算出来的答案可能是$\textrm{20.57512321,}$他们实际上都指向了$\textrm{20.5}$这个特征值,但是如果直接进行比较,他们的结果是不等的,因此我们需要进行四舍五入。但是具体的位数很难敲定,因为$\textrm{20.4475634}$与$\textrm{20.57512321}$又很有可能是真的两个不同 的特征值,所以我们仍旧是期待一种较为理想的状态$\textrm{:}$即任意两个不同的特征值之间有足够的距离。而关于$\textrm{LU}$分 解不存在的情况,我们可以稍微倾斜一下平移距离,倾斜的大小又回到了精度$\textrm{:}$平移的距离大小相对特征值本身的规模而言是否在同一个数量级。分治解决该问题也许不是最佳,又或者矩阵的全部特征值本就不会用反幂法来求解,这里主要是提供一种思路。在比较理想的假设下,我设计一个$\textrm{PowerMethod}$的类$\textrm{(c++)}$,设计了上述思路的实现。其中记录特征值的容器选用了$\textrm{STL}$的哈希表$\textrm{-unordered_map}$,向量的实现使用了$\textrm{STL}$的$\textrm{vector}$,矩阵则是采用了二维$\textrm{vector}$。类的成员有注释说明,成员函数可以参照函数名观察用途。
#ifndef PROJECT1_POWERMETHOD_H
#define PROJECT1_POWERMETHOD_H
#include <vector>
#include <iostream>
#include <cmath>
#include <unordered_map>
#include <unordered_set>
using namespace std;
class PowerMethod{
private:
int size; //Size of matrix
double eps; //End condition
int count; //write down the times of iteration
int maxCount; //Maximum times of loops
vector<vector<double>> matrix; //Input data
vector<double> initIteration; //The start of iteration
double MaxEigenValue; //Maximum eigenvalue by module
double MinEigenValue; //Minimum eigenvalue by module
vector<double> MaxEigenVector; //Maximum eigenvector by module
vector<double> MinEigenVector; //Minimum eigenvector by module
vector<vector<double>> L,U; //Triangular decomposition
unordered_map<double,vector<double>> Hash; //All (EigenValue,EigenVector) pair
public:
//Algorithm related
vector<double> Mult(vector<vector<double>> ,vector<double>);
bool Judge(vector<double> ,vector<double>);
bool calculateLU();
vector<double> solveEquationsByLU(vector<double>);
bool solveMaxEigen(double);
bool solveMinEigen(double);
unordered_map<double,vector<double>> getAllEigenValue();
void solveAllEigenValue(double left,double right);
//init, input, get, set & print
PowerMethod();
void init();
void setSize(int);
int getSize();
void inputMatrix();
vector<vector<double>> getMartix();
void setMatrix(vector<vector<double>>);
double getEps();
void setEps(double);
int getCount();
void setMaxCount(int);
int getMaxCount();
double getMaxEigenValue();
double getMinEigenValue();
vector<double> getMaxEigenVector();
vector<double> getMinEigenVector();
void inputInitIteration();
void setInitIteration(vector<double>);
void setDefalutIteration();
vector<double> getInitIteration();
vector<vector<double>> getL();
vector<vector<double>> getU();
void Print(vector<vector<double>>);
void Print(vector<double>);
};
#endif //PROJECT1_POWERMETHOD_H
#include "PowerMethod.h"
PowerMethod::PowerMethod()
{
size = 1;
eps = 1e-5;
maxCount = 10000;
MinEigenValue = MaxEigenValue = 0;
init();
}
void PowerMethod::setSize(int _size)
{
size = _size;
init();
}
int PowerMethod::getSize()
{
return size;
}
void PowerMethod::init()
{
matrix.resize(size);
for(int i = 0;i < size;i++)
matrix[i].resize(size);
initIteration.resize(size);
setDefalutIteration();
}
void PowerMethod::inputMatrix()
{
for(int i = 0;i < size;i++)
for(int j = 0;j < size;j++)
cin>>matrix[i][j];
calculateLU();
}
vector<vector<double>> PowerMethod::getMartix()
{
return matrix;
}
void PowerMethod::setMatrix(vector<vector<double>> _matrix)
{
matrix = _matrix;
calculateLU();
}
double PowerMethod::getEps()
{
return eps;
}
void PowerMethod::setEps(double _eps)
{
eps = _eps;
}
int PowerMethod::getCount()
{
return count;
}
void PowerMethod::setMaxCount(int _maxCount)
{
maxCount = _maxCount;
}
int PowerMethod::getMaxCount()
{
return maxCount;
}
double PowerMethod::getMaxEigenValue()
{
return MaxEigenValue;
}
double PowerMethod::getMinEigenValue()
{
return MinEigenValue;
}
vector<double> PowerMethod::getMaxEigenVector()
{
return MaxEigenVector;
}
vector<double> PowerMethod::getMinEigenVector()
{
return MinEigenVector;
}
void PowerMethod::inputInitIteration()
{
for(int i = 0;i < size;i++)
cin>>initIteration[i];
}
void PowerMethod::setInitIteration(vector<double> _initIteraiton)
{
initIteration = _initIteraiton;
}
void PowerMethod::setDefalutIteration()
{
for(int i = 0;i < initIteration.size();i++)
initIteration[i] = 1;
}
vector<double> PowerMethod::getInitIteration()
{
return initIteration;
}
vector<vector<double>> PowerMethod::getL()
{
return L;
}
vector<vector<double>> PowerMethod::getU()
{
return U;
}
void PowerMethod::Print(vector<vector<double>> a)
{
for(auto array:a)
{
for(auto e: array)
cout<<e<<" ";
cout<<endl;
}
cout<<endl;
}
void PowerMethod::Print(vector<double> a)
{
for(auto e: a)
cout<<e<<" ";
cout<<"\n"<<endl;
}
vector<double> PowerMethod::Mult(vector<vector<double>> a,vector<double>b)
{
int n = a.size();
vector<double> result(n);
for(int i = 0;i < n;i++)
{
result[i] = 0;
for(int j = 0;j < n;j++)
result[i] += a[i][j]*b[j];
}
return result;
}
bool PowerMethod::calculateLU()
{
int n = size;
L.resize(n); U.resize(n);
for(int i = 0;i < n;i++) L[i].resize(n);
for(int i = 0;i < n;i++) U[i].resize(n);
for(int i = 0;i < n;i++) L[i][i] = 1;
for(int k = 0;k < n;k++)
{
for(int j = k;j < n;j++)
{
double sum = 0;
for(int r = 0;r < k;r++) sum += L[k][r]*U[r][j];
U[k][j] = matrix[k][j] - sum;
//if(isnan(U[k][j]) || isinf(U[k][j])) return false;
}
for(int i = k+1;i < n;i++)
{
double sum = 0;
for(int r = 0;r < k;r++) sum += L[i][r]*U[r][k];
L[i][k] = (matrix[i][k] - sum)/U[k][k];
//if(isnan(L[i][k]) || isinf(L[i][k])) return false;
}
}
return true;
}
vector<double> PowerMethod::solveEquationsByLU(vector<double> b)
{
int n = size;
vector<double> x(n),y(n);
for(int i = 0;i < n;i++)
{
double sum = 0;
for(int j = 0;j < i;j++) sum += L[i][j]*y[j];
y[i] = b[i]-sum;
}
for(int i = n-1;i >= 0;i--)
{
double sum = 0;
for(int j = i+1;j < n;j++) sum += U[i][j]*x[j];
x[i] = (y[i]-sum)/U[i][i];
}
return x;
}
bool PowerMethod::Judge(vector<double> a,vector<double> b)
{
int n = b.size();
double cmp = a[0]/b[0];
for(int i = 1;i < n;i++)
if(fabs(cmp-a[i]/b[i]) > eps)
return false;
return true;
}
bool PowerMethod::solveMaxEigen(double speedup)
{
bool f = true;
int n = matrix.size();
for(int i = 0;i < n;i++) matrix[i][i] -= speedup;
vector<double> X,Y;
Y = initIteration;
X = Mult(matrix,Y);
count = 0;
while(!Judge(X,Y))
{
double maxv = fabs(X[0]);
for(int i = 1;i < X.size();i++) maxv = max(maxv,fabs(X[i]));
for(int i = 0;i < Y.size();i++) Y[i] = X[i]/maxv;
X = Mult(matrix,Y);
count++;
if(count == maxCount)
{
f = false;
break;
}
}
MaxEigenValue = (X[0]/Y[0])+speedup;
if(isnan(MaxEigenValue) || isinf(MaxEigenValue)) f = false;
MaxEigenVector = Y;
for(int i = 0;i < n;i++) matrix[i][i] += speedup;
return f;
}
bool PowerMethod::solveMinEigen(double speedup)
{
int n = matrix.size();
for(int i = 0;i < n;i++) matrix[i][i] -= speedup;
if(!calculateLU())
{
for(int i = 0;i < n;i++) matrix[i][i] += speedup;
return false;
}
bool f = true;
vector<double> X,Y;
Y = initIteration;
X = solveEquationsByLU(Y);
count = 0;
while(!Judge(X,Y))
{
double maxv = fabs(X[0]);
for(int i = 1;i < X.size();i++) maxv = max(maxv,fabs(X[i]));
for(int i = 0;i < Y.size();i++) Y[i] = X[i]/maxv;
X = solveEquationsByLU(Y);
count++;
if(count == maxCount)
{
f = false;
break;
}
}
MinEigenValue = (Y[0]/X[0])+speedup;
if(isnan(MinEigenValue) || isinf(MinEigenValue)) f = false;
MinEigenVector = Y;
for(int i = 0;i < n;i++) matrix[i][i] += speedup;
return f;
}
unordered_set<double> tmp;
unordered_map<double,vector<double>> PowerMethod::getAllEigenValue()
{
Hash.clear();
double right,left;
if(!solveMaxEigen(0)) right = 1e9;
else right = abs(MaxEigenValue);
left = -right;
solveAllEigenValue(left,right);
for(auto it = tmp.begin();it != tmp.end();it++)
{
solveMinEigen(*it);
Hash[MinEigenValue] = MinEigenVector;
}
return Hash;
}
void PowerMethod::solveAllEigenValue(double left,double right)
{
int k = 10;
while(!solveMinEigen(left)) left -= 0.5;
double l = round(MinEigenValue*k)/k;
while(!solveMinEigen(right)) right += 0.5;
double r = round(MinEigenValue*k)/k;
if(l == r)
{
if(!tmp.count(l)) tmp.insert(l);
return ;
}
double mid = (left+right)/2;
solveAllEigenValue(left,mid-0.1);
solveAllEigenValue(mid+0.1,right);
}
这里再给出一个测试样例的结果,测试矩阵:
$$ \begin{bmatrix} 4&-2&7&3&-1&8\\-2&5&1&1&4&7\\7&1&7&2&3&5\\3&1&2&6&5&1\\-1&4&3&5&3&2\\8&7&5&1&2&4 \end{bmatrix} $$
测试结果:
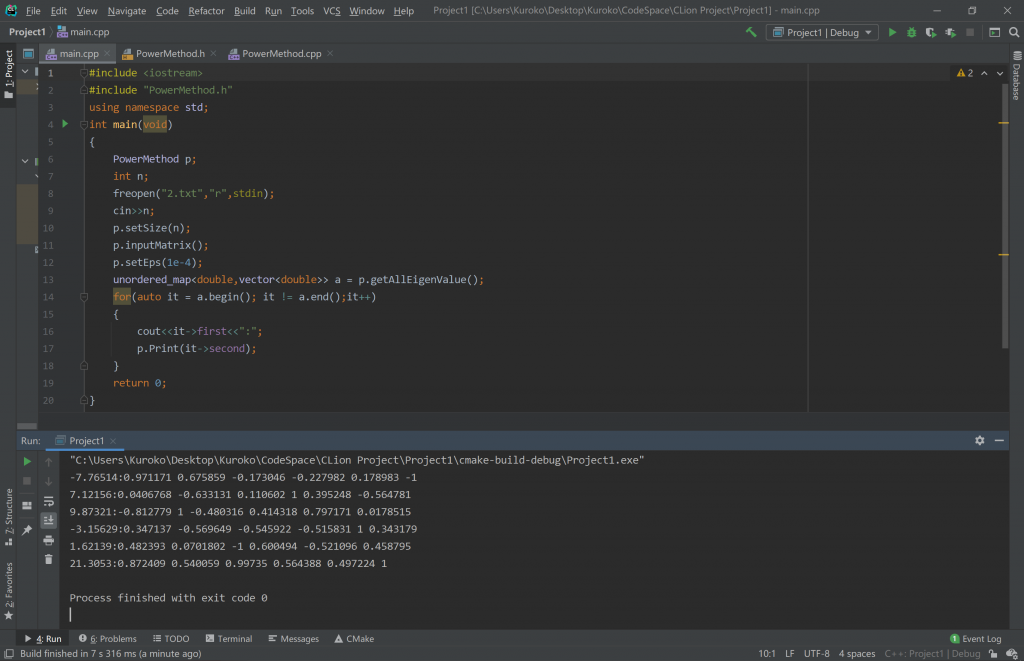
Author@Kuroko
GitHub@SuperKuroko
LeetCode@kuroko177
Last Modified: 2020-12-30 19:15